**Improving Mujoco-MJX with First Principles**
Han Wang
October 20th, 2024
[Han's Blog](https://hansolowang.com)
TLDR: Current MJX implementation of quaternion multiplication is not efficient on the GPU. Re-implementing quaternion multiplication with a GPU friendly method leads to noticeable improvements in compile and execution time.
# Background
Last year Mujoco released [Mujoco XLA](https://mujoco.readthedocs.io/en/stable/mjx.html#). A JAX implementation of physics simulation. MJX is best for simulating in parallel on the GPU. However, while profiling an MJX simulation of kuka_iiwa14 on GPU. I noticed that the forward kinematics is unusually slow. The jit time of forward kinematics is 1.83s and the execution time is 0.00213s, over 20x slower than the python binding of the C implementation....
Code
```
model_path = "kuka_iiwa_14/iiwa14.xml"
mjc_m = mujoco.MjModel.from_xml_path(model_path)
mjc_d = mujoco.MjData(mjc_m)
mjx_m = mjx.put_model(mjc_m)
mjx_d = mjx.make_data(mjx_m)
mjc_d = mujoco.mj_kinematics(mjc_m, mjc_d) # 0.0001s
jit_kinematics = jax.jit(mjx.kinematics)
f_jitted = jax.jit(mjx.kinematics).lower(mjx_m, mjx_d).compile() # 1.83s compile time
mjx_d = f_jitted(mjx_m, mjx_d) # 0.00213s execution time
# The timings are the average of 1000 runs each.
```
I get it, there can be a lot of explanations here: the GPU is not good with branching, JAX overhead, expensive memory transfers between host and device, etc. Anyways, I thought this was worth digging deeper.
# Digging Deeper
`jax.jit` can be broken down to the following stages:
- python callable -> jaxpr -> HLO -> executable.
Let's see what the intermediate stages look like under the hood .
kinematics jaxpr: 7100 lines
kinematics hlo: 5300 lines
Not very helpful... My brain is too smooth to retrieve useful information from the thousand of lines of intermediate jaxpr and hlo.
If there is somehow a way to associate each jaxpr or hlo with the originating python code, then it might be more useful. So if you know any useful static/dynamics instrumentation tools for JAX please let me know.
# Applying First Principles Thinking
OK, lets use first principles (probably should have started with this first :p)
Forward kinematics at the basic level is coordinate transformations down a chain. You apply a translation and a rotation at each link. Translation is addition. Rotation is more complex. In MJX, its done with quaternion multiplication. The implementation is the standard 28 floating point operations.
When we dig deeper and peek the HLO of the MJX implementation. Woah... for those 28 floating point operations, we have 96 hlo operations. The majority of them are memory operations, slicing and reshaping.
Ok, lets avoid the memory operations by reimplementing quaternion multiplications as [matrix-matrix multiplications](https://en.wikipedia.org/wiki/Quaternion#Matrix_representations). It will be over 200 floating point operations instead of 28, but should save us memory expenses.
CODE for quat mul with matrices
```
QUAT_MULTIPLY = np.zeros((4, 4, 4), dtype=np.float64)
QUAT_MULTIPLY[:, :, 0] = [[ 1, 0, 0, 0],
[ 0,-1, 0, 0],
[ 0, 0,-1, 0],
[ 0, 0, 0,-1]]
QUAT_MULTIPLY[:, :, 1] = [[ 0, 1, 0, 0],
[ 1, 0, 0, 0],
[ 0, 0, 0, 1],
[ 0, 0,-1, 0]]
QUAT_MULTIPLY[:, :, 2] = [[ 0, 0, 1, 0],
[ 0, 0, 0,-1],
[ 1, 0, 0, 0],
[ 0, 1, 0, 0]]
QUAT_MULTIPLY[:, :, 3] = [[ 0, 0, 0, 1],
[ 0, 0, 1, 0],
[ 0,-1, 0, 0],
[ 1, 0, 0, 0]]
def quat_mul(u: jax.Array, v: jax.Array) -> jax.Array:
return jnp.sum(
QUAT_MULTIPLY *
u[..., :, None, None] *
v[..., None, :, None],
axis=(-3, -2))
```
The hlo for quaternion multiplication with matrices is only 8 operations (WOW, 96 -> 8). Not as many memory operations too.
Let's compare the memory performance with Nsight Compute
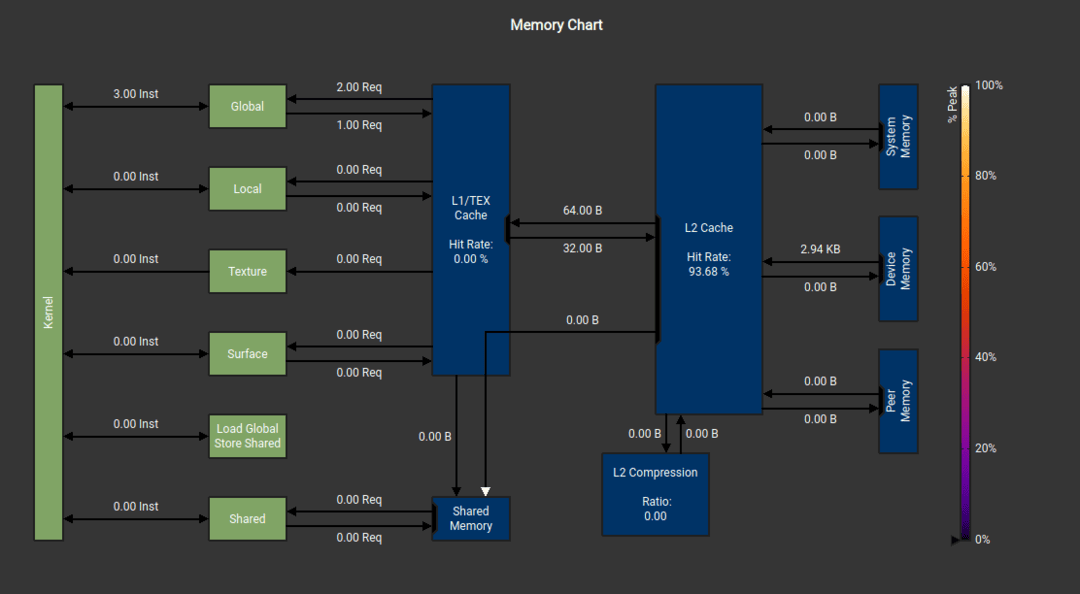MJX implementation of quaternion multiplication (0% L1 hit rate...)
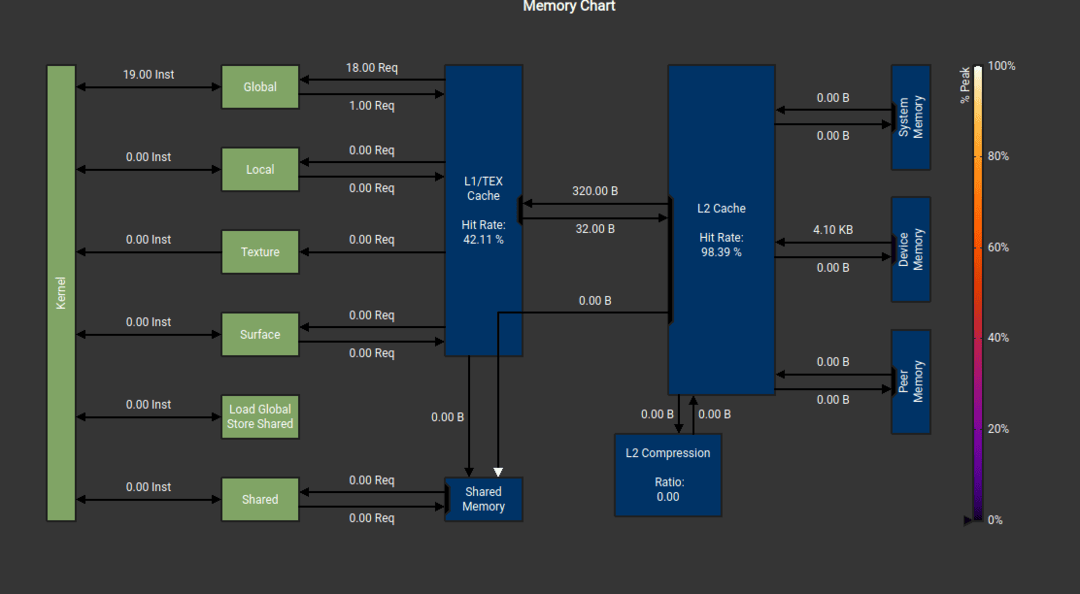Matrix implementation of quaternion multiplication (42% L1 hit rate)
The compile time of `mjx.kinematics` with this new implementation is now 1.28s, a 30% improvement from original implementation. This can be explained by the the smaller number of HLO operations, which means less JAX overhead. Runtime is 0.00201s now, a 6% improvement.
Ok, forward kinematics is only a small part of a simulation loop. How much improvement are we seeing with respect to a full simulation loop
Code and comparison results
```
```
jax.config.update("jax_enable_x64", True)
NUM_STEPS = 1000
key = jax.random.key(0)
print(f"jax is using {jax.default_backend()}")
model_path = "kuka_iiwa_14/iiwa14.xml"
mjc_m = mujoco.MjModel.from_xml_path(model_path)
mjc_d = mujoco.MjData(mjc_m)
mjx_m = mjx.put_model(mjc_m)
mjx_d = mjx.make_data(mjx_m)
@jax.jit
def step(data, ctrl):
data = data.replace(ctrl=ctrl)
carry = mjx.step(mjx_m, data)
return carry, carry
controls = jax.random.uniform(key, shape=(NUM_STEPS, mjx_m.nu), minval=-1.0, maxval=1.0)
# compiling
# old implementation: 3.93s
# new implementation: 3.23s (18% improvement)
_ = step(mjx_d, jax.random.uniform(key, shape=(mjx_m.nu)))
# simulation loop
# old implementation: 1.37s
# new implementation: 1.26s (8% improvement)
final, stacked = jax.lax.scan(step, mjx_d, controls)
# Avg of 100 runs
```
# Conclusion
The math functions in `mjx._src.math.py` are 1 to 1 reimplementation of C Mujoco (potentially other parts of MJX too). The C implementations have been carefully optimize for CPU and might does not transfer well to the GPU programming paradigm.
Future work will be identifying such code and writing a GPU friendly version. The [rotate method](https://github.com/google-deepmind/mujoco/blob/476599f8b6175ef5a3040c47ebb3cd99a83c5365/mjx/mujoco/mjx/_src/math.py#L102) looks like a low hanging fruit. Perhaps we can get additional speedup if rotations were specified with matrices instead of quaternions. The trade off would be the need of constant re-orthanormalizing, a larger memory footprint, numerical errors at small angles, etc. We also need to consider [Amdahl's law](https://en.wikipedia.org/wiki/Amdahl%27s_law), the most expensive part of an MJX simulation loop is collision detection *by far*. Goodness me! Its 2:43am, I should stop rambling. Good night...
mjx version: 3.2.3. CPU: i7-12th gen GPU: 3070